L’algèbre booléenne est une branche des mathématiques qui traite des opérations logiques sur des variables booléennes. Les variables booléennes ne peuvent prendre que deux valeurs: vrai (1) ou faux (0). L’algèbre booléenne est largement utilisée en informatique, en électronique, en logique, en mathématiques, et dans d’autres domaines où les valeurs logiques sont importantes.

Les tableaux de Karnaughs sont une méthode graphique pour simplifier les expressions booléennes. Ils permettent de réduire le nombre de termes dans une expression logique en regroupant les termes qui ont des valeurs identiques.

Les processeurs c’est quasiment que ça. C’est des circuits logiques qui font des opérations booléennes (ET, OU, NON) sur des bits (0 ou 1). Les circuits logiques sont construits à partir de transistors, qui sont des composants électroniques qui peuvent être utilisés pour contrôler le flux de courant électrique. Les transistors peuvent être utilisés pour construire des portes logiques, qui sont des circuits électroniques qui effectuent des opérations logiques sur des signaux binaires.

C’est George Boole qui a introduit l’algèbre booléenne en 1854. Il a montré que les opérations logiques peuvent être exprimées en termes d’opérations algébriques sur des variables booléennes. L’algèbre booléenne est basée sur les opérations logiques de base: ET (AND), OU (OR), et NON (NOT).

Le système algébrique est constitué de l’ensemble $\{0, 1\}$, des opérations ET (AND, a.b, ab), OU (OR, a+b), et NON (NOT, $\overline{a}$, $\neg a$), et des règles de simplification.

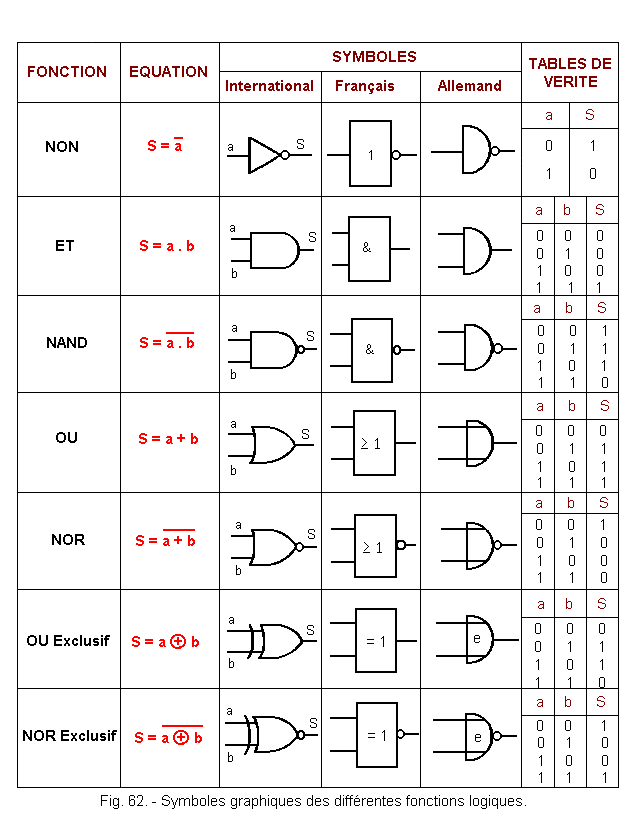
Exemple avec les operateurs “NAND” et “NOR”:

$$NAND(a, b) = \overline{a.b} = \overline{a} + \overline{b} \\ NOR(a, b) = \overline{a+b} = \overline{a} . \overline{b}$$

a	b	$\overline{a}$	$\overline{b}$	a.b	$\overline{a.b}$	a+b	$\overline{a+b}$	$\overline{a} + \overline{b}$	$\overline{a} . \overline{b}$
1	1	0	0	1	0	1	0	0	0
1	0	0	1	0	1	1	0	1	0
0	1	1	0	0	1	1	0	1	0
0	0	1	1	0	1	0	1	1	1

Propriétés:

• Involution: $\overline{\overline{a}} = a$
• Idempotence: $a.a = a$
• Compleméntarité: $a.\overline{a} = 0$ et $a + \overline{a} = 1$
• Associativité: $(a.b).c = a.(b.c)$ et $(a+b)+c = a+(b+c)$
• Elements neutres: $a.1 = a$ et $a+0 = a$
• Distributivité: $a.(b+c) = a.b + a.c$ et $a+(b.c) = (a+b).(a+c)$
• Absorption: $a.(a+b) = a$ et $a+(a.b) = a$
• De Morgan: $\overline{a+b} = \overline{a}.\overline{b}$ et $\overline{a.b} = \overline{a} + \overline{b}$
• Associativité: $(a+b+c) = a+(b+c)$ et $(a.b.c) = a.(b.c)$

---

Fonctions booléennes

Une fonction booléenne est une fonction qui prend des variables booléennes en entrée et renvoie une valeur booléenne en sortie. Les variables booléennes peuvent être combinées à l’aide d’opérations logiques pour former des expressions booléennes. Les fonctions booléennes sont souvent utilisées pour représenter des circuits logiques et des systèmes de contrôle.

Les fonctions booléennes peuvent être représentées sous forme de table de vérité ou d’expression logique. Une table de vérité est un tableau qui montre toutes les combinaisons possibles de valeurs d’entrée et les valeurs de sortie correspondantes. Une expression logique est une expression algébrique qui décrit la fonction booléenne en termes d’opérations logiques.

Pour une fonction logique à 𝑛 variables :

• min-terms: groupe des 𝑛 variables liées par des ET
• max-terms: groupe des 𝑛 variables liées par des OU Forme canonique d’une fonction logique :
• première forme canonique: union (OU) de mintermes
• deuxième forme canonique: intersection (ET) de maxtermes Il n’y a qu’une seule expression d’une forme canonique de chaque type pour une fonction donnée.

Soit la fonction $f$ a trois variables $a$, $b$, et $c$:

• min-terms: $abc, a\overline{b}c, a\overline{b}\overline{c}, \overline{a}bc, \cdots$
• max-terms: $a+b+c, a+\overline{b}+c, a+\overline{b}+\overline{c}, \overline{a}+b+c, \overline{a}+b+\overline{c}, \cdots$
• premiere forme canonique: $f(a, b, c) = abc + a\overline{b}c + a\overline{b}\overline{c} + \cdots$
• deuxieme forme canonique: $f(a, b, c) = (a+b+c).(a+\overline{b}+c).(a+\overline{b}+\overline{c}).(\overline{a}+b+c).\cdots$

Faisons un exercice: Soit la fonction $f(a, b, c) = ab + \overline{b}c + a\overline{c}$.

a	b	c	$\overline{b}$	$\overline{c}$	ab	$\overline{b}c$	$a\overline{c}$	$f$
1	1	1	0	0	1	0	0	1
1	1	0	0	1	1	0	1	1
1	0	1	1	0	0	1	0	1
1	0	0	1	1	0	0	1	1
0	1	1	0	0	0	0	0	0
0	1	0	0	1	0	0	0	0
0	0	1	1	0	0	1	0	1
0	0	0	1	1	0	0	0	0

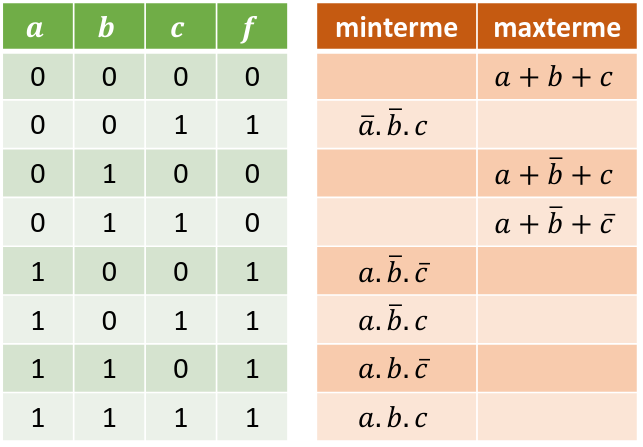
Un autre: soit la fonction $f(a, b, c) = ac + b\overline{c}$

a	b	c	$\overline{c}$	ac	$b\overline{c}$	$f$	minterme	maxterme
1	1	1	0	1	0	1	1	1
1	1	0	1	0	1	1	2	2
1	0	1	0	1	0	1	4	4
1	0	0	1	0	0	0	0	0
0	1	1	0	0	0	0	0	0
0	1	0	1	0	1	1	2	2
0	0	1	0	0	0	0	0	0
0	0	0	1	0	0	0	0	0

Comment trouver les minterme et maxterme ? En gros les minterm c’est le groupe des 𝑛 variables liées par des ET et mes maxterm sont des groupe des 𝑛 variables liées par des OU.

---

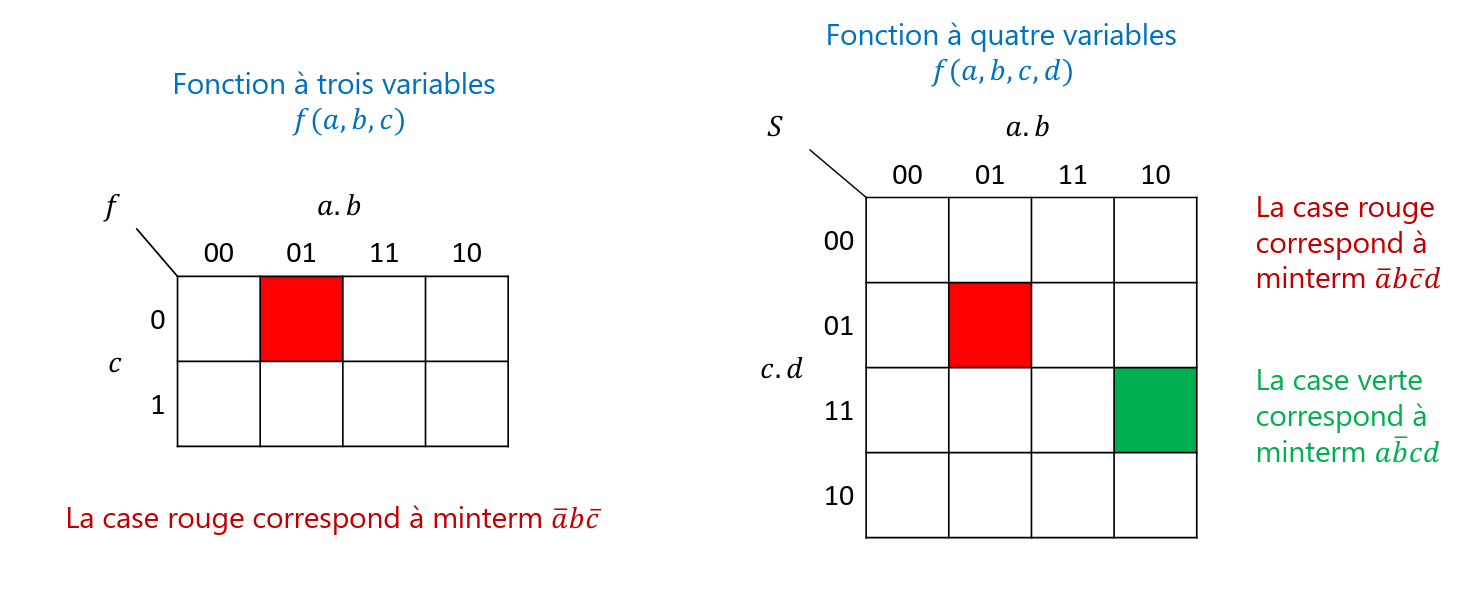
Tableaux de Karnaughs

Les tableaux de Karnaughs sont une méthode graphique pour simplifier les expressions booléennes. Ils permettent de réduire le nombre de termes dans une expression logique en regroupant les termes qui ont des valeurs identiques. Les tableaux de Karnaughs sont particulièrement utiles pour simplifier les fonctions booléennes avec un petit nombre de variables.