Exponentielle

Il existe une unique fonction $f$ dérivables sur $\mathbb{R}$ telle que $f(0) = 1$ et $f'(x) = f(x)$ pour tout $x \in \mathbb{R}$. Cette fonction est appelée la fonction exponentielle et est notée $f(x) = e^x$.

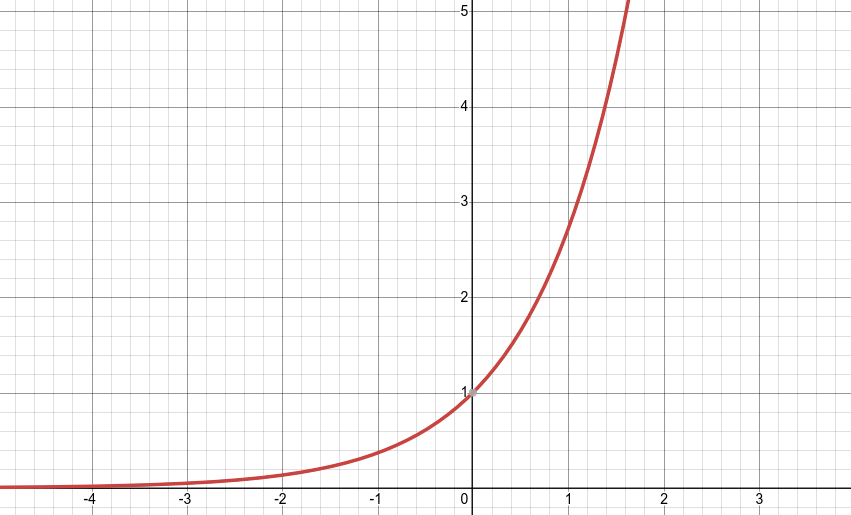
La fonction exponentielle est une fonction croissante, c’est-à-dire que pour tout $x \in \mathbb{R}$, $e^x > 0$.
Le nombre $e$ est une constante qui vaut environ $2.71$.

• C’est un nombre irrationnel, c’est-à-dire qu’il ne peut pas être exprimé comme une fraction.
• C’est une des constantes les plus importantes en mathématiques, car elle est la base des logarithmes naturels.
• $e$ est le langage naturel de la croissance exponentielle.
• Le mathématicien suisse Leonhard Euler a démontré que $e$ est égal à $2.71$ grâce à la formule suivante:

$$e = 1 + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \ldots$$

• $e$ rassemble toutes les constantes mathématiques les plus connues dans la formule d’Euler:

$$e^{i\pi} + 1 = 0$$

• Si on prend un point sur le graphe de $e^x$, on peut voir que la tangente à ce point est égale à la fonction elle-même. C’est une des propriétés les plus importantes de la fonction exponentielle.
  

Les propriétés

Théorème: Pour tout $x, y \in \mathbb{R}$, $e^{x+y} = e^x \cdot e^y$.
Corolaires:

• $e^{-x} = \frac{1}{e^x}$.
• $e^{nx} = (e^x)^n$, pour tout $n \in \mathbb{N}$.
• $e^{x-y} = \frac{e^x}{e^y}$.
• $e^0 = 1$.
• $e^1 = e$.

Dérivée de la fonction exponentielle

La dérivée de la fonction exponentielle est la fonction elle-même. C’est-à-dire que pour tout $x \in \mathbb{R}$, $(e^x)' = e^x$.

Exemple:

$$f(x) = (x + 1)e^x$$ $$f'(x) = 1 \cdot e^x + (x + 1)e^x$$ $$f'(x) = e^x(1 + x + 1)$$ $$f'(x) = e^x(2 + x)$$ $$\begin{array}{|c|c|c|} \hline x & -\infty & +\infty \\ \hline f'(x) & + & + \\ \hline f(x) & 0 & +\infty \\ \hline \end{array}$$

Fonction forme $f(x) = e^{kx}, k \in \mathbb{R}$

La fonction $f(x) = e^{kx}$ est dérivée de la fonction exponentielle. C’est-à-dire que pour tout $x \in \mathbb{R}$, $(e^{kx})' = ke^{kx}$.

**Exemple**: $$f(x) = e^{2x}$$ $$f'(x) = 2e^{2x}$$

A savoir que $(e^{u(x)})' = u'(x)e^{u(x)}$.

Aussi, $(ln(u(x)))' = \frac{u'(x)}{u(x)}$.

---