Théorie des graphes
Le problème des sept ponts de Königsberg (aujourd’hui Kaliningrad, Russie) résolu par Leonhard Euler en 1736 est à l’origine de la théorie des graphes.
Ce problème consiste à déterminer s’il existe ou non une promenade dans les rues de Königsberg permettant, à partir d’un point de départ au choix, de passer une et une seule fois par chaque pont, et de revenir à son point de départ, étant entendu qu’on ne peut traverser la rivière Pregel qu’en passant sur les ponts.
De manière générale, un graphe permet de représenter la structure, les connexions d’un ensemble complexe en expriment les relations entre les éléments de cet ensemble: reseaux de communication, réseaux routiers, circuits électriques etc.
Dans un graphe, on distingue les sommets et les arêtes ou arcs. Ce sont les éléments de base d’un graphe. Un sommet est un point du graphe, une arête est une liaison entre deux sommets.
Graphes non orientés
Un graphe non orienté est un graphe dont les arêtes n’ont pas de direction. On peut les représenter par des lignes ou des segments de droites.
Un graphe fini est défini par l’ensemble fin dont les éléments sont appelés sommets, et par l’ensemble fini dont les éléments sont appelés arêtes.
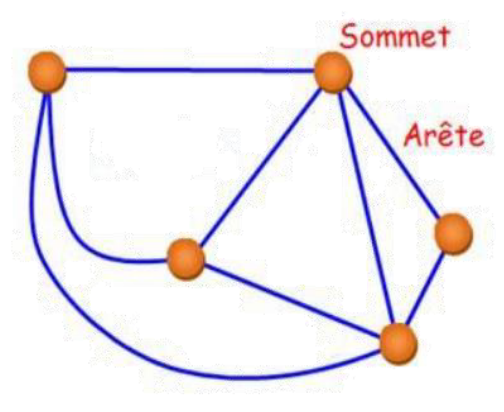
Si on peut dessiner un graphe 𝐺 dans le plan sans qu’aucune arête n’en coupe une autre (les arêtes ne sont pas forcément rectilignes), on dit que 𝐺 est planaire.
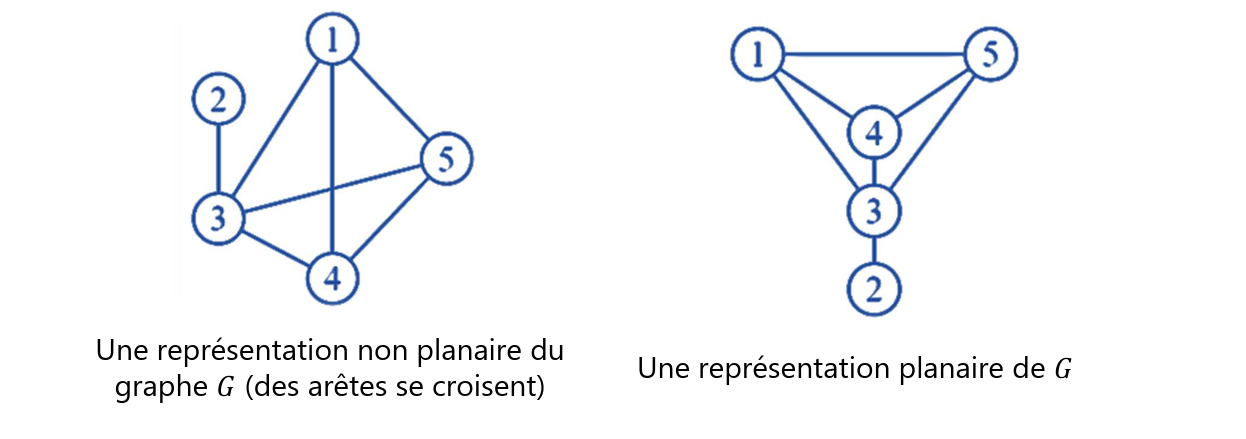
Un graphe est simple si au plus une arête relie deux sommets et s’il n’y a pas de boucle sur un sommet.
On peut imaginer des graphes avec une arête qui relie un sommet à lui-même (une boucle), ou plusieurs arêtes reliant les deux mêmes sommets. On appellera ces graphes des multigraphes.
Un graphe est connexe s’il est possible, à partir de n’importe quel sommet, de rejoindre tous les autres en suivant les arêtes.
Un graphe non connexe se décompose en composantes connexes.

Un graphe est complet si chaque sommet du graphe est relié directement à tous les autres sommets.
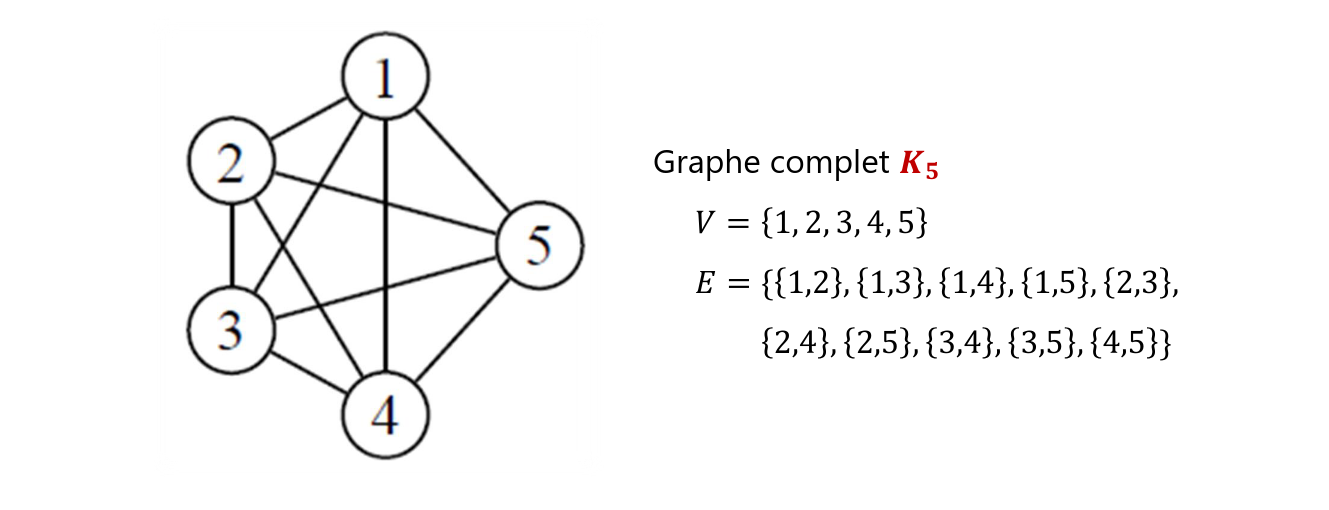
Un graphe est biparti si ses sommets peuvent être divisés en deux ensembles et , de sorte que toutes les arêtes du graphe relient un sommet dans à un sommet dans .

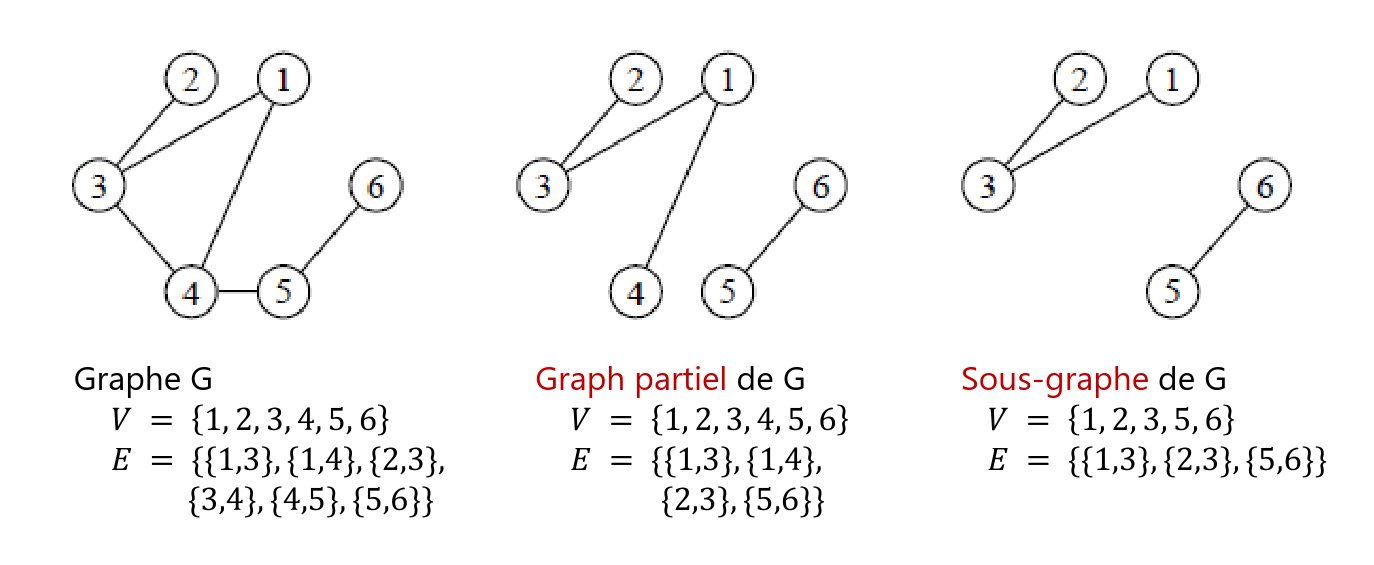
Soit un graphe. Le graphe est un graphe partiel de si .
Pour un sous-ensemble de sommets inclus dans , le sous-graphe de induit par est le graphe dont l’ensemble des sommets est et l’ensemble des arêtes est formé de toutes les arêtes de ayant leurs deux extrémités dans . Autrement dit, on obtient en enlevant un ou plusieurs sommets au graphe , ainsi que toutes les arêtes incidentes à ces sommets.
On appelle clique un sous-graphe complet de 𝐺.
On appelle degré du sommet , et on note , le nombre d’arêtes incidentes à ce sommet. Attention ! Une boucle sur un sommet compte double.
Dans un graphe simple, on peut aussi définir le degré d’un sommet comme étant le nombre de ses voisins (la taille de son voisinage). Dans le multigraphe ci-contre, on a les degrés :
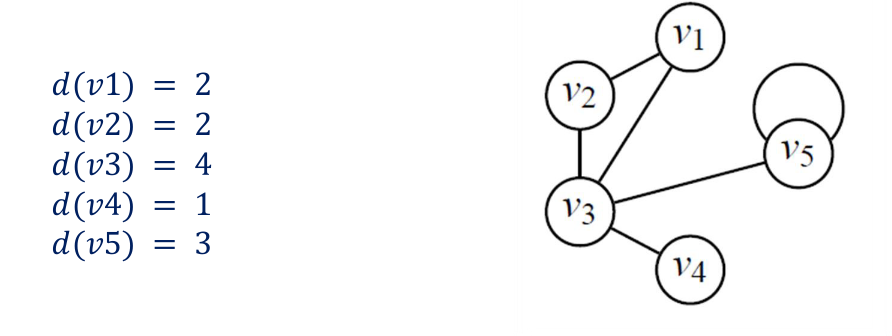
Le degré d’un graphe est le degré maximum de tous ses sommets. Dans l’exemple ci-dessous, le degré du graphe est 4, à cause du sommet .
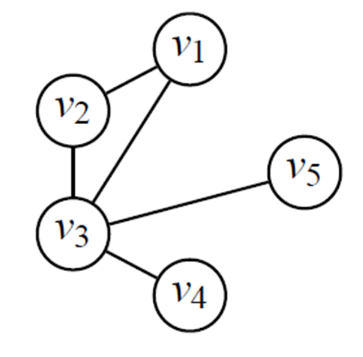
Un graphe dont tous les sommets ont le même degré est dit régulier. Si le degré commun est , alors on dit que le graphe est 𝒌-régulier.
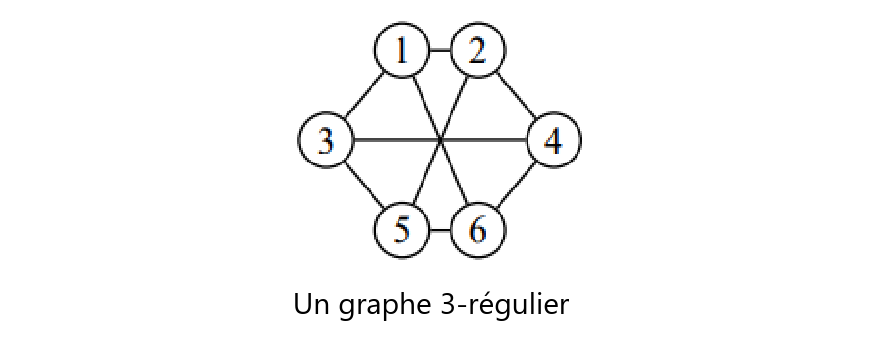
Théorème : La somme des degrés des sommets d’un graphe est égale à deux fois le nombre d’arêtes.
Une suite décroissante (au sens large) d’entiers est graphique s’il existe un graphe simple dont les degrés des sommets correspondent à cette suite.
Une chaîne dans , est une suite ayant pour éléments alternativement des sommets et des arêtes, commençant et se terminant par un sommet, et telle que chaque arête est encadrée par ses extrémités. On dira que la chaîne a pour longueur le nombre d’arêtes de la chaîne. Le graphe ci-dessous contient, entre autres, les chaînes :
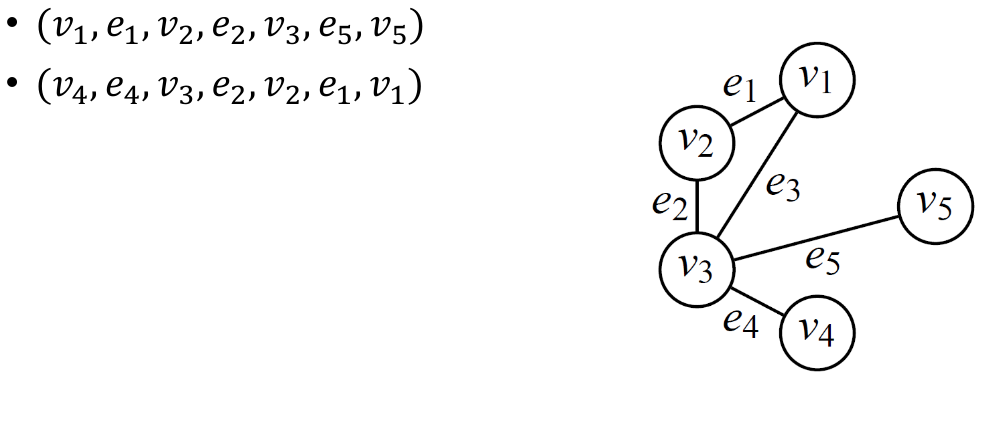
- On appelle distance entre deux sommets la longueur de la plus petite chaîne les reliant.
- On appelle diamètre d’un graphe la plus longue des distances entre deux sommets
- Une chaîne est élémentaire si chaque sommet y apparaît au plus une fois.
- Une chaîne est simple si chaque arête apparaît au plus une fois.
- Une chaîne dont les sommets de départ et de fin sont les mêmes est appelée chaîne fermée.
- Une chaîne fermée simple est appelée cycle.
Théorème : Pour un graphe ayant arêtes, sommets et composantes connexes, on définit :
est appelé le nombre cyclomatique. Prononcer « nu de G ».
On a pour tout graphe . si et seulement si est sans cycle.
On appelle cycle eulérien d’un graphe un cycle passant une et une seule fois par chacune des arêtes de . Un graphe est dit eulérien s’il possède un cycle eulérien.
On appelle chaîne eulérienne d’un graphe une chaîne passant une et une seule fois par chacune des arêtes de . Un graphe est dit semi-eulérien s’il possède une chaîne eulérienne.
Un graphe ne possédant que des chaînes eulériennes est semi-eulérien.
Plus simplement, on peut dire qu’un graphe est eulérien (ou semi-eulérien) s’il est possible de dessiner le graphe sans lever le crayon et sans passer deux fois sur la même arête.
Un graphe est eulérien s’il est connexe et si tous ses sommets sont de degré pair.
Il est semi-eulérien si tous ses sommets sauf deux sont de degré pair; les chaînes eulériennes du graphe auront alors ces deux sommets pour extrémités.
On appelle cycle hamiltonien d’un graphe un cycle passant une et une seule fois par chacun des sommets de . Un graphe est dit hamiltonien s’il possède un cycle hamiltonien.
On appelle chaîne hamiltonienne d’un graphe une chaîne passant une et une seule fois par chacun des sommets de .
Contrairement aux graphes eulériens, il n’existe pas de caractérisation simple des graphes hamiltoniens. On peut énoncer quelques propriétés et conditions suffisantes :
- Un graphe possédant un sommet de degré 1 ne peut pas être hamiltonien
- Si un sommet dans un graphe est de degré 2, alors les deux arêtes incidentes à ce sommet doivent faire partie du cycle hamiltonien
- Les graphes complets sont hamiltoniens
Soit un graphe simple. Un couplage de est un sous-graphe partiel 1-régulier de . On peut aussi dire qu’un couplage est un ensemble d’arêtes deux à deux non-adjacentes.
Un sommet est saturé par un couplage si est l’extrémité d’une arête de . Dans le cas contraire, est insaturé.
Un couplage maximum est un couplage contenant le plus grand nombre possible d’arêtes. Un graphe peut posséder plusieurs couplages maximum.

Un couplage parfait est un couplage où chaque sommet du graphe est saturé.

Si est un couplage de , on appelle chaîne alternée une chaîne élémentaire de dont les arêtes sont alternativement dans et hors de .
Une chaîne alternée est dite augmentante si elle relie deux sommets insaturés. Ci-dessus, à gauche, la chaîne 1-4-3-6 est augmentante.
On dit qu’un graphe est planaire si on peut le dessiner dans le plan de sorte que ses arêtes ne se croisent pas. Rappelons que les arêtes ne sont pas forcément rectilignes.
Une carte, ou graphe planaire topologique, est une représentation particulière d’un multigraphe planaire fini.

Théorème : La somme des degrés des régions d’une carte connexe est égale à deux fois le nombre d’arêtes.
Théorème (Euler, 1752) : Euler a établi une formule célèbre qui relie le nombre de sommets 𝑆, le nombre d’arêtes 𝐴 et le nombre de régions 𝑅 d’une carte connexe :
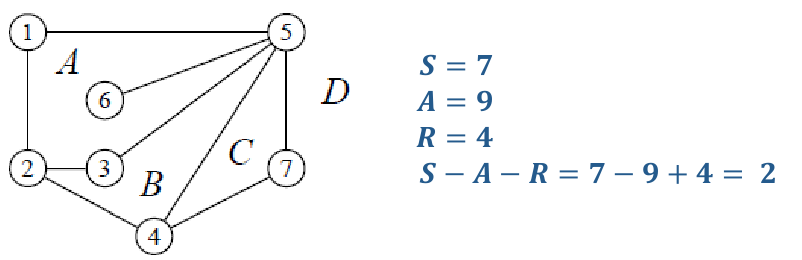
Représentations non-graphiques d’un graphe
Un graphe peut être représenté de manière non-graphique par une matrice d’adjacence ou une liste d’adjacence. Une matrice est un tableau de lignes et colonnes.Dans une matrice d’adjacences, les lignes et les colonnes représentent les sommets du graphe. Un « 𝟏 » à la position signifie que le sommet est adjacent au sommet .
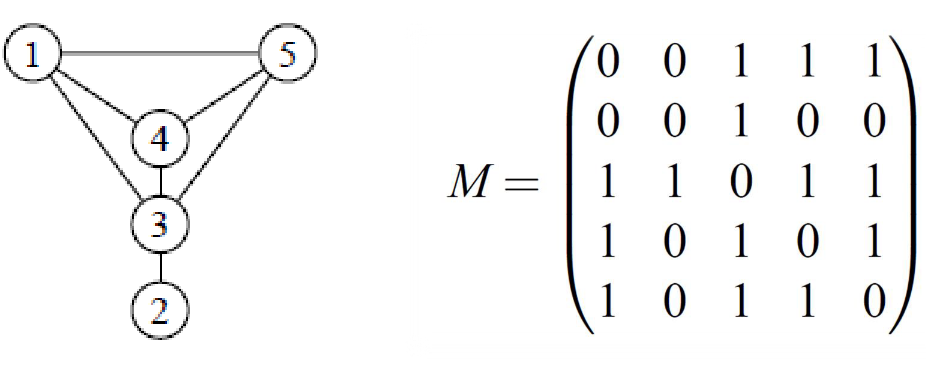
On peut aussi représenter un graphe simple en donnant pour chacun de ses sommets la liste des sommets auxquels il est adjacent. Ce sont les listes d’adjacences.
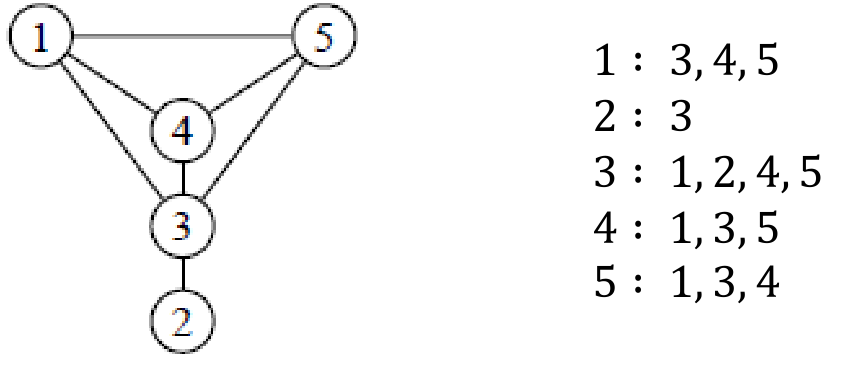
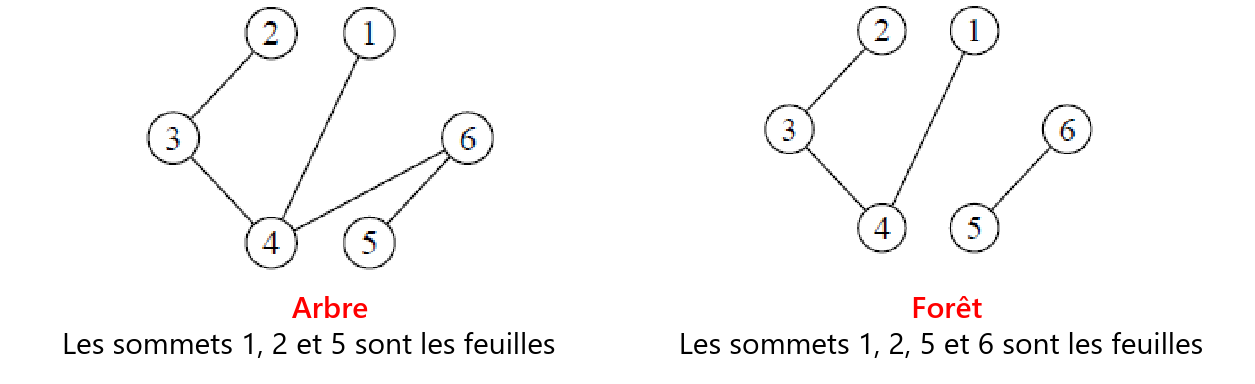
On appelle arbre tout graphe connexe sans cycle.
Un graphe sans cycle mais non connexe est appelé une forêt.
Une feuille ou sommet pendant est un sommet de degré 1.
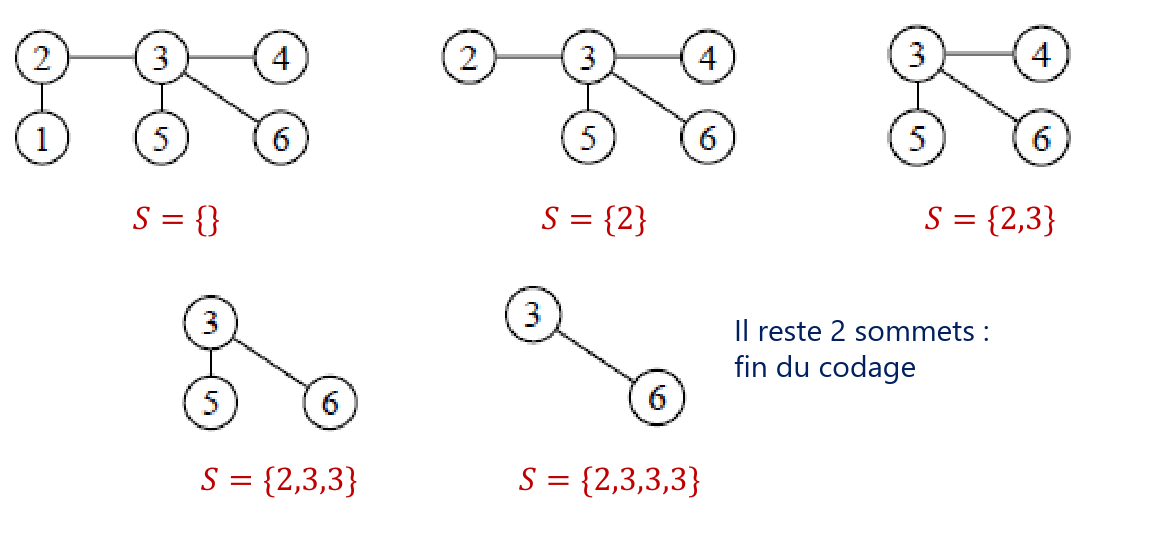
Codage de Prüfer : Soit un arbre étiqueté à sommets. On peut associer à une suite de entiers entre 1 et de la manière suivante :
- On supprime les feuilles de une à une, en les ajoutant à la suite.
- On répète l’opération jusqu’à ce qu’il ne reste plus que deux sommets dans .
- On ajoute alors l’unique arête reliant ces deux sommets à la suite.
- La suite obtenue est le codage de Prüfer de .
On peut également effectuer un décodage de Prüfer pour retrouver l’arbre étiqueté à partir de la suite de Prüfer.
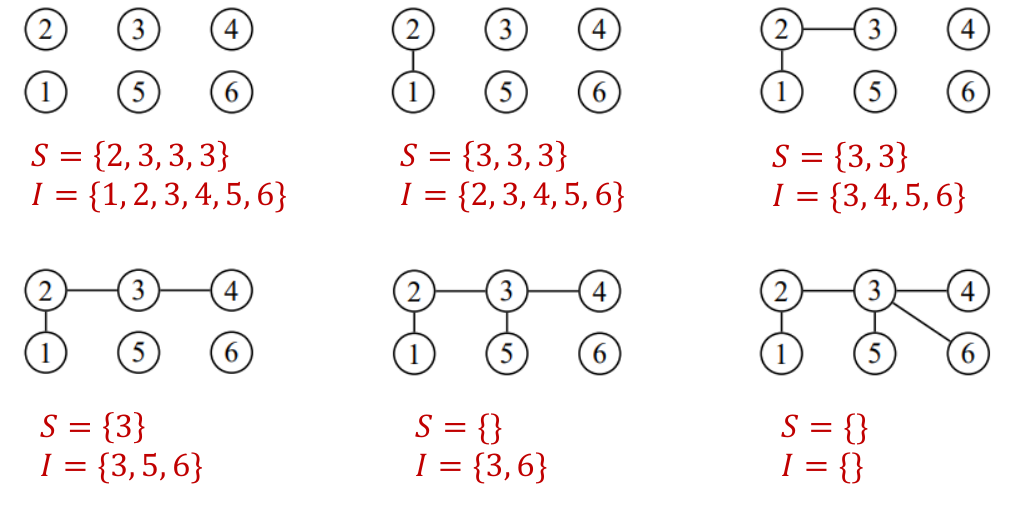
Le nombre chromatique d’un graphe est le nombre minimum de couleurs nécessaires pour colorier les sommets de telle sorte que deux sommets adjacents n’aient pas la même couleur.
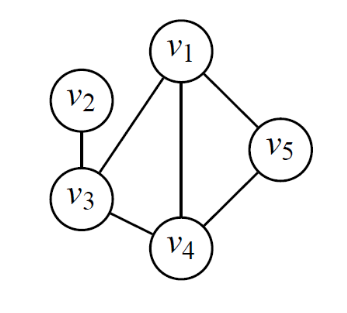
Soit un graphe. Un sous ensemble de est un stable s’il ne comprend que des sommets non adjacents deux à deux. Dans le graphe ci-dessous, et forment un stable. et aussi.
Le cardinal du plus grand stable est le nombre de stabilité de . On le note . Dans le graphe ci dessous, on a
Le nombre chromatique :
où est le degré maximum du graphe et est l’ordre de sa plus grande clique
Graphes orientés
En donnant un sens aux arêtes d’un graphe, on obtient un digraphe (ou graphe orienté). Le mot « digraphe » est la contraction de l’expression anglaise « directed graph ».
Un digraphe fini est défini par l’ensemble fini dont les éléments sont appelés sommets, et par l’ensemble fini dont les éléments sont appelés arcs.
Un arc de l’ensemble est défini par une paire ordonnée de sommets. Lorsque , on dit que l’arc va de a et que est l’origine de et l’extrémité de .
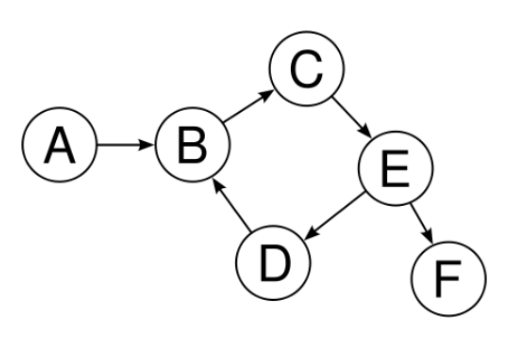
Soit un sommet d’un graphe orienté.
On note le degré exterieur du sommet , c’est-à-dire le nombre d’arcs ayant 𝑣 comme extrémité initiale.
On note le degré intérieur du sommet , c’est-à-dire le nombre d’arcs ayant 𝑣 comme extrémité finale.
On définit le degré:
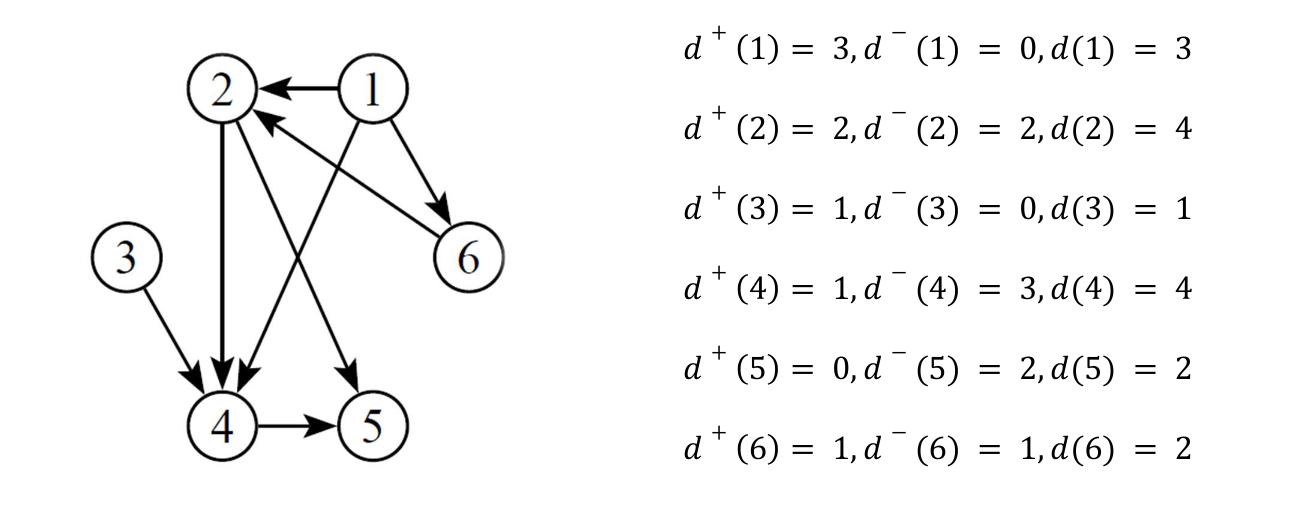
Un chemin conduisant du sommet au sommet est une suite ayant pour éléments alternativement des sommets et des arcs, commençant et se terminant par un sommet, et telle que chaque arc est encadré à gauche par son sommet origine et à droite par son sommet destination. On ne peut donc pas prendre les arc à rebours.
Sur le digraphe ci-dessous, on peut voir par exemple le chemin .
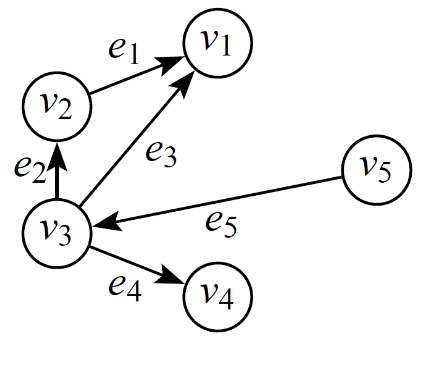
Par convention, tout chemin comporte au moins un arc.
On appelle distance entre deux sommets d’un digraphe la longueur du plus petit chemin les reliant. S’il n’existe pas de chemin entre les sommets et , on pose .
Un circuit est un chemin dont les sommets de départ et de fin sont les mêmes.
Le digraphe ci-dessus ne contient pas de circuit.
Les notions de chemins et de circuits sont analogues à celles des chaînes et des cycles pour les graphes non orientés.
On peut représenter un digraphe par une matrice d’adjacences.
Dans une matrice d’adjacences, les lignes et les colonnes représentent les sommets du graphe. Un « 1 » à la position signifie qu’il existe un arc allant de à .
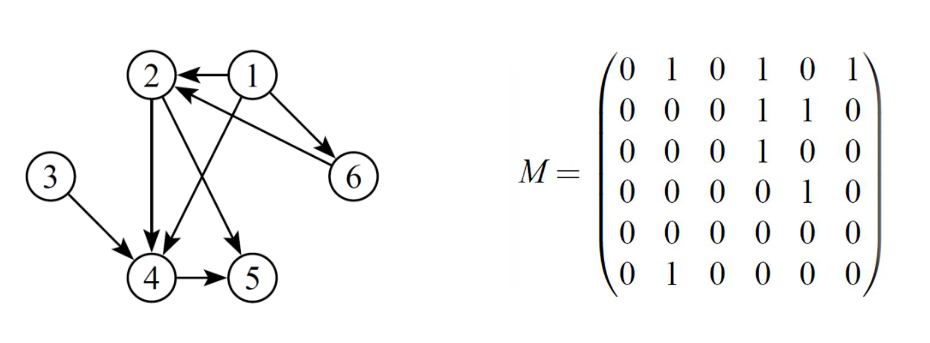
On peut aussi représenter un digraphe en donnant pour chacun de ses sommets la liste des sommets qu’on peut atteindre directement en suivant un arc (dans le sens de la flèche). Par exemple, pour le même graph qu’au dessus:
- 1: 2, 4, 6
- 2: 4, 5
- 3: 4
- 4: 5
- 5: -
- 6: 2
Le digraphe 𝐺 est sans circuit si et seulement si on peut attribuer un nombre appelé le rang de 𝒗, à chaque sommet de manière que pour tout arc de on ait
L’algorithme de Dijkstra permet de trouver le plus court chemin entre deux sommets d’un graphe (orienté ou non orienté).
Dans l’exemple du graphe ci-dessous, on va rechercher le chemin le plus court menant de M à S.
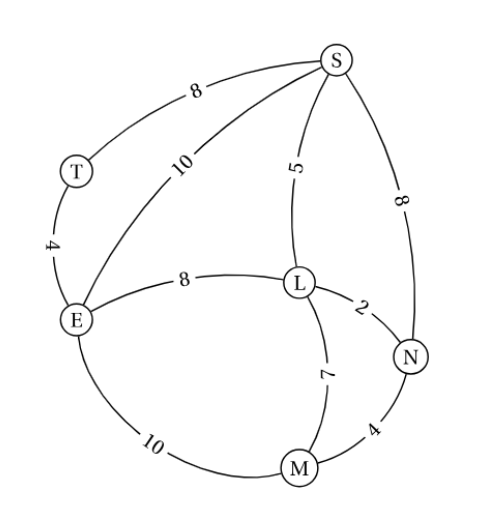
On construit un tableau ayant pour colonnes chacun des sommets du graphe. On ajoute à gauche une colonne qui recensera les sommets choisis à chaque étape. Puisque l’on part du sommet M, on inscrit, sur la première ligne intitulée « Départ », dans la colonne M et dans les autres colonnes.
| Départ | E | L | M | N | S | T |
|---|---|---|---|---|---|---|
| M |
À partir de M, on voit sur le graphe que l’on peut rejoindre E, L et N en respectivement 10, 7 et 4 minutes. Ces durées sont les durées les plus courtes ; elles sont inférieures au durées inscrites sur la ligne précédente qui étaient «∞».
| Départ | E | L | M | N | S | T |
|---|---|---|---|---|---|---|
| Départ | ||||||
| M (0) |
On sélectionne le plus petit résultat de la dernière ligne. Ici, c’est « » qui correspond au chemin menant au sommet N en 4 minutes.
- On met en évidence cette sélection.
- On inscrit le sommet retenu et la durée correspondante dans la première colonne : N (4).
- On désactive les cases situées en dessous de notre sélection. On a trouvé le trajet le plus court menant à N ; il dure 4 minutes.
| Départ | E | L | M | N | S | T |
|---|---|---|---|---|---|---|
| Départ | ||||||
| M (0) | X | |||||
| N (4) | X | X |
À partir de N, on peut rejoindre L et S (on ne se préoccupe plus de M qui a été « désactivé »).
- Si l’on rejoint L : On mettra 2 minutes pour aller de N à L et 4 minutes pour aller de M à N, soit au total 6 minutes. On indique donc 𝟔𝑵 dans la colonne L. Le N situé en indice signifie que l’on vient du sommet N.
- Si l’on rejoint S : On mettra 8 minutes pour aller de N à S et 4 minutes pour aller de M à N, soit au total 12 minutes. On indique donc 𝟏𝟐𝑵 dans la colonne S.
| Départ | E | L | M | N | S | T |
|---|---|---|---|---|---|---|
| Départ | ||||||
| M (0) | X | |||||
| N (4) | X | X |
On sélectionne le plus petit résultat de la dernière ligne. Ici, c’est « » qui correspond au chemin menant au sommet L en 6 minutes.
- On met en évidence cette sélection.
- On inscrit le sommet retenu et la durée correspondante dans la première colonne : L (6).
- On désactive les cases situées en dessous de notre sélection. On a trouvé le trajet le plus court menant à L ; il dure 6 minutes.
| Départ | E | L | M | N | S | T |
|---|---|---|---|---|---|---|
| Départ | ||||||
| M (0) | X | |||||
| N (4) | X | X | ||||
| L (6) | X | X | X |
À partir de L, on peut rejoindre E et S (on ne se préoccupe plus de M ni de N qui ont été « désactivés »).
- Si l’on rejoint E : On mettra 14 minutes au total (8 minutes de L à E + 6 minutes de M à L). Ce trajet N’EST PAS plus rapide que le précédent qui durait 10 minutes; on recopie le contenu précédent 𝟏𝟎𝑴 dans la colonne E
- Si l’on rejoint S : On mettra 11 minutes au total (5 minutes de L à S + 6 minutes de M à L). Ce trajet est plus rapide que le précédent qui durait 12 minutes. On indique donc 𝟏𝟏𝑳 dans la colonne S
| Départ | E | L | M | N | S | T |
|---|---|---|---|---|---|---|
| Départ | ||||||
| M (0) | X | |||||
| N (4) | X | X | ||||
| L (6) | X | X | X |
On sélectionne le plus petit résultat. Ici, c’est « » qui correspond au chemin menant au sommet E en 10 minutes.
| Départ | E | L | M | N | S | T |
|---|---|---|---|---|---|---|
| Départ | ||||||
| M (0) | X | |||||
| N (4) | X | X | ||||
| L (6) | X | X | X | |||
| E (10) | X | X | X | X |
On sélectionne le plus petit résultat. C’est « » qui correspond au chemin menant au sommet S en 11 minutes. On a trouvé le trajet le plus court menant à S : il dure 11 minutes.
| Départ | E | L | M | N | S | T |
|---|---|---|---|---|---|---|
| Départ | ||||||
| M (0) | X | |||||
| N (4) | X | X | ||||
| L (6) | X | X | X | |||
| E (10) | X | X | X | X |
Il reste toutefois à reconstituer le trajet qui correspond à cette durée de 11 minutes.
- On part de notre point d’arrivée : S
- On recherche la cellule marquée en rouge de la colonne S ; elle contient . On note la lettre écrite en indice : L.
- On recherche la cellule marquée en rouge de la colonne L ; elle contient . On note la lettre écrite en indice : N.
- On recherche la cellule marquée en rouge de la colonne N ; elle contient . On note la lettre écrite en indice : M.
- On est arrivé à notre point de départ M après être passé par N et L et S (liste obtenue en listant les sommets en ordre inverse).
Le trajet optimal est donc M - N - L - S.