Github

Fonctions du second degré

On peut calculer les coordonnées du sommet d'une parabole de la forme f(x)=ax2+bx+cf(x) = ax^2 + bx + c avec la formule suivante:

xs=−b2ax_s = -\frac{b}{2a} ys=f(xs)y_s = f(x_s)

L'axe de symétrie de la parabole est la droite d'équation x=xsx = x_s.

Le sommet de la parabole est donc le point de coordonnées (xs,ys)(x_s, y_s).

On peut également calculer le discriminant Δ\Delta de la parabole avec la formule suivante:

Δ=b2−4ac\Delta = b^2 - 4ac

Le discriminant permet de déterminer le nombre de solutions de l'équation f(x)=0f(x) = 0:

  • Si Δ>0\Delta > 0, l'équation a deux solutions réelles distinctes.
  • Si Δ=0\Delta = 0, l'équation a une solution réelle double.
  • Si Δ<0\Delta < 0, l'équation n'a pas de solution réelle.

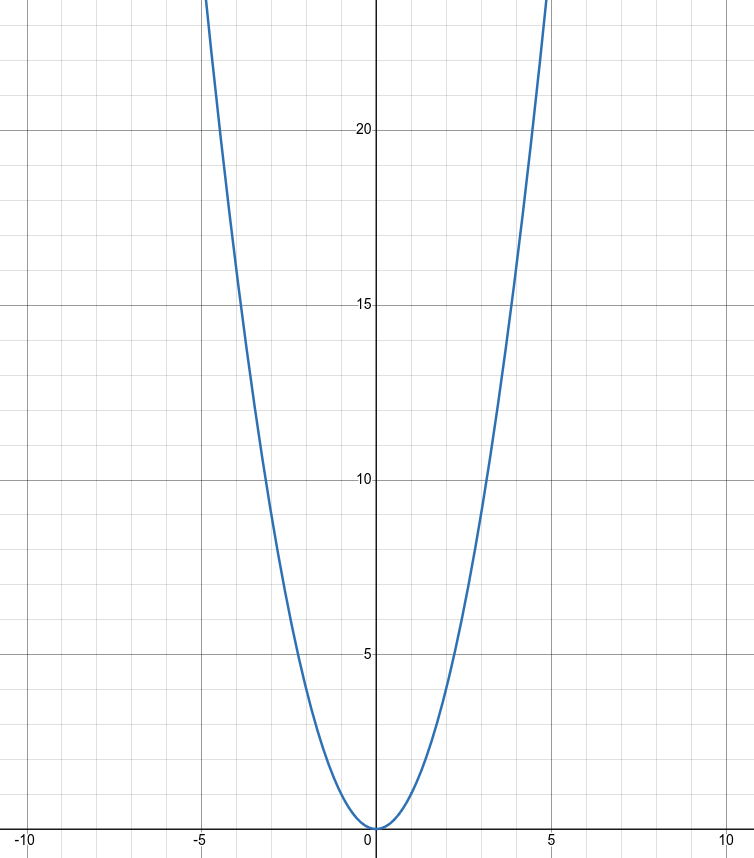
La représentation graphique de la fonction du second degré est la suivante :

Diagram