Logarithme népérien

Le logarithme népérien est le logarithme en base $e$. Il est noté $\ln(x)$.

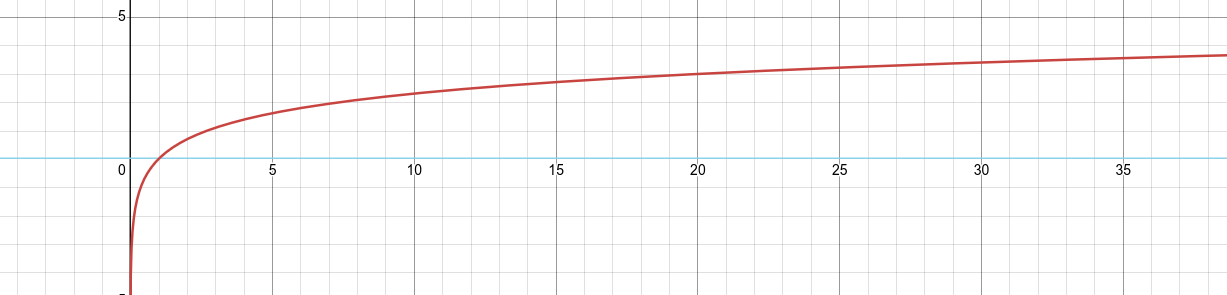
Le logarithme népérien est l'inverse de la fonction exponentielle. C'est-à-dire que pour tout $x > 0$, $\ln(e^x) = x$.

Le logarithme népérien est une fonction croissante, c'est-à-dire que pour tout $x > 0$, $\ln(x) > 0$.

Quelques propriétés du logarithme népérien:

• $\ln(1) = 0$.
• $\ln(e) = 1$.
• $\ln(\frac{1}{x}) = -\ln(x)$.
• $\ln(\frac{x}{y}) = \ln(x) - \ln(y)$.
• $\ln(x)^n = n\ln(x)$.
• $\ln(\sqrt{x}) = \frac{1}{2}\ln(x)$.

Exemple: Simplifier les expressions suivantes:

$$A = ln(3 - \sqrt(5)) + ln(3 + \sqrt(5))$$ $$A = ln((3 - \sqrt(5))(3 + \sqrt(5)))$$ $$A = ln(9 - 5)$$ $$A = ln(4)$$

Dérivation

La dérivée du logarithme népérien est donnée par la formule suivante:

$$\ln(x) = \frac{1}{x}$$

Exemple: Calculer la dérivée de la fonction $f(x) = \ln(1 - 2x + x^2)$.

$$u = 1 - 2x + x^2$$ $$u' = -2 + 2x$$ $$f'(x) = \frac{u'}{u} = \frac{-2 + 2x}{1 - 2x + x^2}$$