Les fonctions affines et linéaires

Définition : Pour tout $x$ dans $\mathbb{R}$, une fonction affine est définie par ( f(x) = ax + b ), où ( a ) et ( b ) sont des réels donnés.

• ( a ) est appelé le coefficient directeur (ou pente) et indique la direction de la fonction.
• ( b ) est l'ordonnée à l'origine, le point où la droite croise l'axe des ordonnées.

Si ( b = 0 ), la fonction est dite linéaire.

Variations

• Croissante : Si ( a > 0 ), la fonction est croissante.
• Décroissante : Si ( a < 0 ), la fonction est décroissante.
• Constante : Si ( a = 0 ), la fonction est constante.

Signe de ( f(x) )

$x$	$-\infty$	$0$	$+\infty$
$f(x)$	+	-	+

Représentation graphique

Exemple 1 : Fonction constante

Soit la fonction ( f(x) = 2 ).
La fonction est constante, donc horizontale. Peu importe la variation de ( x ), ( f(x) ) reste égal à 2.

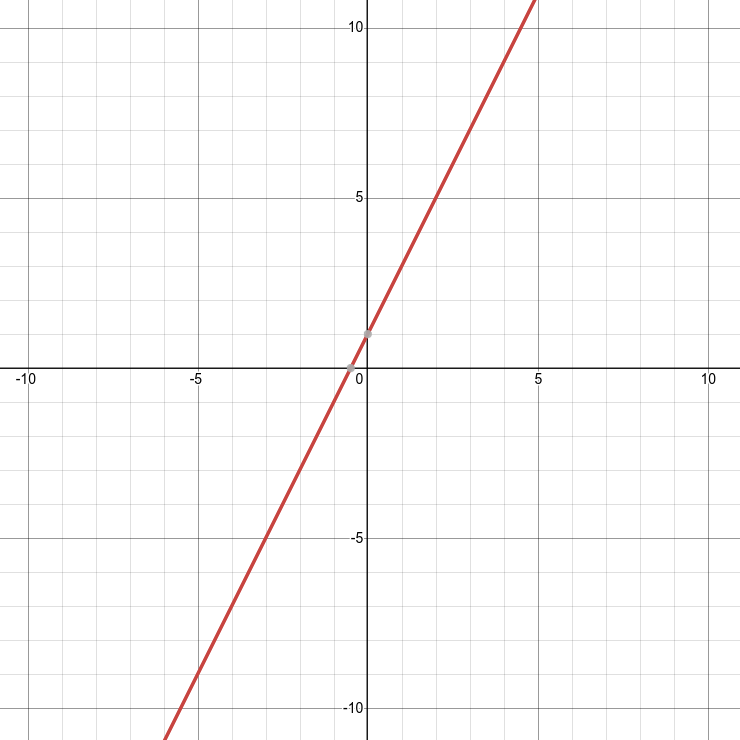
Exemple 1.2 : Fonction linéaire

Considérons la fonction ( f(x) = 2x ).
C'est une droite passant par l'origine et elle est croissante car ( a > 0 ).

Tableau des valeurs :

$x$	$f(x)$
0	0
1	2
2	4
3	6

Exemple 1.3 : Comparaison de tarifs de taxi

• Taxi 1 : 5€ de prise en charge, 0.40€ par km. ( f(x) = 5 + 0.40x )

• Taxi 2 : Pas de prise en charge, 0.60€ par km. ( f(x) = 0.60x )

Question 1 : Quel taxi est le moins cher pour 8 km puis pour 30 km ?

Pour ( x = 8 ) :

• Taxi 1 : ( f(8) = 5 + 0.40 \times 8 = 8.20€ )
• Taxi 2 : ( f(8) = 0.60 \times 8 = 4.80€ )

Pour ( x = 30 ) :

• Taxi 1 : ( f(30) = 5 + 0.40 \times 30 = 17€ )
• Taxi 2 : ( f(30) = 0.60 \times 30 = 18€ )

Conclusion : Taxi 1 est le moins cher pour 8 km, et Taxi 2 est le moins cher pour 30 km.

Question 2 : Un client dispose de 12€, combien de km peut-il parcourir avec chaque taxi ?

Pour ( f(x) = 12€ ) :

• Taxi 1 : ( 12 = 5 + 0.40x )
  [ 12 - 5 = 0.40x \implies 7 = 0.40x \implies x = 17.5 km ]

• Taxi 2 : ( 12 = 0.60x )
  [ x = \frac120.6 = 20 km ]

Conclusion : Le client peut parcourir 17.5 km avec Taxi 1 et 20 km avec Taxi 2.

Exercice : Tarifs d'entrée d'un stade de football

• Tarif 1 : 8€
• Tarif 2 : 4€ avec la carte demi-tarif qui coûte 40€
• Tarif 3 : Abonnement pour la saison à 92€

Question 1 : Calculer la dépense pour 6, 11, et 15 entrées pour chaque tarif et déterminer le tarif le plus avantageux.

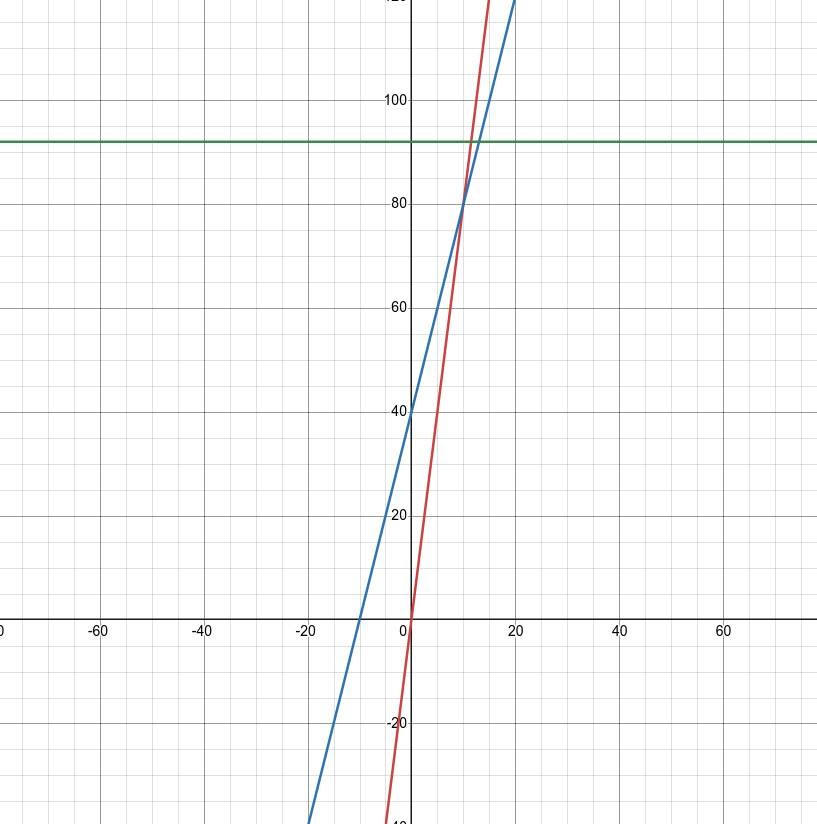
Réponse 1 :

• Tarif 1 : ( f(x) = 8x )
• Tarif 2 : ( f(x) = 4x + 40 )
• Tarif 3 : ( f(x) = 92 )

Pour ( x = 6 ) :

• Tarif 1 : ( f(6) = 8 \times 6 = 48€ )
• Tarif 2 : ( f(6) = 4 \times 6 + 40 = 64€ )
• Tarif 3 : ( f(6) = 92€ )

Pour ( x = 11 ) :

• Tarif 1 : ( f(11) = 8 \times 11 = 88€ )
• Tarif 2 : ( f(11) = 4 \times 11 + 40 = 84€ )
• Tarif 3 : ( f(11) = 92€ )

Pour ( x = 15 ) :

• Tarif 1 : ( f(15) = 8 \times 15 = 120€ )
• Tarif 2 : ( f(15) = 4 \times 15 + 40 = 100€ )
• Tarif 3 : ( f(15) = 92€ )

Conclusion :

• Tarif 1 est le plus avantageux pour 6 entrées.
• Tarif 2 est le plus avantageux pour 11 entrées.
• Tarif 3 est le plus avantageux pour 15 entrées.

Question 2 : Avec le tarif 2, quelle est la dépense pour 18 entrées ?

Réponse 2 :

• Tarif 2 : ( f(x) = 4x + 40 )

Pour ( x = 18 ) :

• ( f(18) = 4 \times 18 + 40 = 112€ )

Conclusion : La dépense pour 18 entrées est de 112€.

Question 3 : Trouver ( x ) tel que ( g(x)=88 ) (Tarif 2). Interpréter le résultat.

Réponse 3 :

• Tarif 2 : ( f(x) = 4x + 40 )

Pour ( f(x) = 88€ ) :

• ( 88 = 4x + 40 )
  [ 88 - 40 = 4x \implies 48 = 4x \implies x = 12 ]

Conclusion : Le client peut acheter 12 entrées avec 88€.

Fonctions valeur absolue

Définition : Pour tout $x$ dans $\mathbb{R}$, la fonction valeur absolue est définie par $f(x) = |x|$.

Exemple

• $f(-2) = |-2| = 2$
• $f(0) = |0| = 0$
• $f(3) = |3| = 3$
• $f(-3) = |-3| = 3$

Représentation graphique

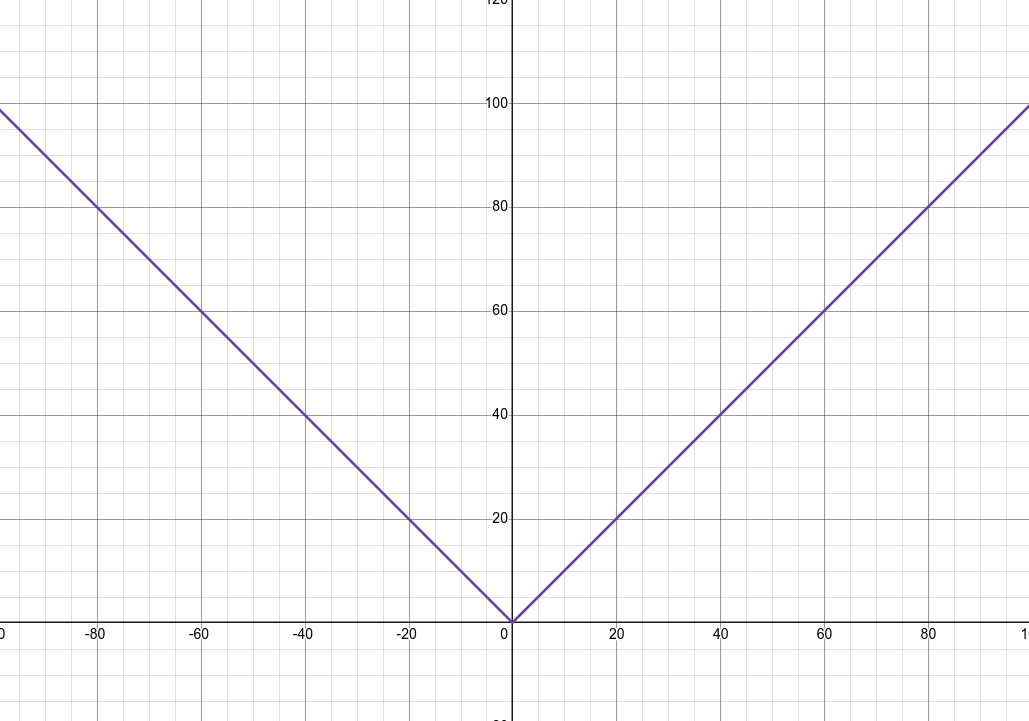
Exemple 2

On modelise une situation dans une fonction qui mesure l'ecart de temps de réponse réel du serveur (en ms) et la valeur idéale de 200ms. La fonction est définie par $f(t) = |t - 200|$.

Question 1: Si un serveur a un temps de réponse de 180ms, quel est l'écart de temps?

Réponse 1:

• $f(t) = |t - 200|$

Si $t = 180$:

• $f(180) = |180 - 200| = |-20| = 20ms$

L'écart de temps est de 20ms.

Question 2: Si un serveur a un temps de réponse de 250ms, quel est l'écart de temps?

Réponse 2:

• $f(t) = |t - 200|$

Si $t = 250$:

• $f(250) = |250 - 200| = |50| = 50ms$

L'écart de temps est de 50ms.

Question 3: Si la tolérance de l'écart de temps est de 30ms, quels sont les écarts de temps acceptables?

Réponse 3:

• $f(t) = |t - 200|$

Si $f(t) = 30$:

• $30 = |t - 200|$

$$30 = |t - 200|$$ $$t - 200 = 30$$ $$t = 230$$

Si $f(t) = -30$:

• $-30 = |t - 200|$

$$-30 = |t - 200|$$ $$t - 200 = -30$$ $$t = 170$$

Les écarts de temps acceptables sont de 170ms à 230ms.

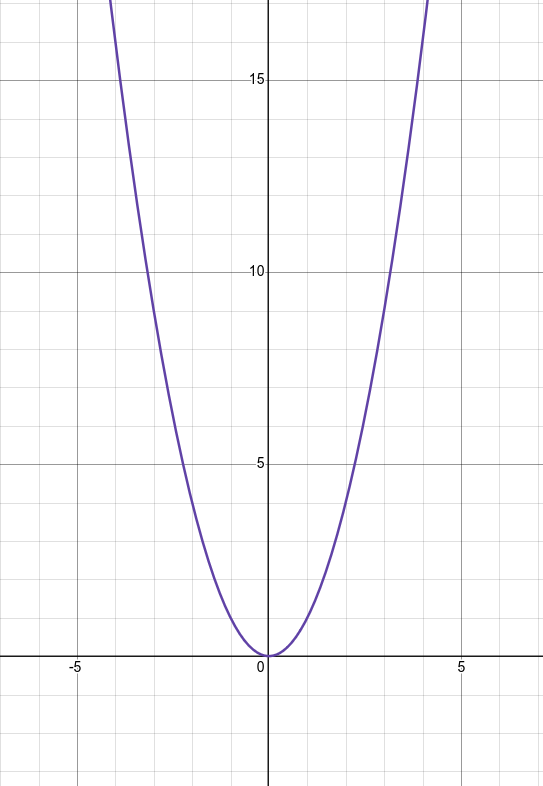
Fonctions carrées

Définition : Pour tout $x$ dans $\mathbb{R}$, la fonction carrée est définie par $f(x) = x^2$.

Exemple

• $f(-2) = (-2)^2 = 4$
• $f(0) = 0^2 = 0$
• $f(3) = 3^2 = 9$
• $f(-3) = (-3)^2 = 9$

Représentation graphique

Les intervalles

• $[0; +\infty[$
• $]-\infty; 0]$
• $]-\infty; +\infty[$

A expliquer

Fonction du second degré

Définition : Pour tout $x$ dans $\mathbb{R}$, la fonction du second degré est définie par $f(x) = ax^2 + bx + c$ où $a$, $b$, et $c$ sont des réels donnés.

Exemple

• $f(x) = 2x^2 + 3x + 1$
• $f(x) = -x^2 + 2x - 3$
• $f(x) = 3x^2 - 4x + 2$

Représentation graphique

On peut calculer les coordonnées du sommet de la parabole avec la formule

$$x = -\frac{b}{2a}$$ $$y = f(x)$$

Le Sommet est le point S(h, k):

$$h = -\frac{b}{2a}$$ $$k = f(h)$$

L'axe de symétrie est la droite verticale passant par le sommet.

Le Delta est le discriminant de l'équation du second degré:

$$\Delta = b^2 - 4ac$$

Si $\Delta > 0$, il y a deux solutions. Si $\Delta = 0$, il y a une solution. Si $\Delta < 0$, il n'y a pas de solution.

Exercice

Vous developpez un jeu vidéo 2D ou le personnage principal lance des boules de feu pour attaquer. La hauteur de la boule de feu est modelisée par la fonction $f(t) = -5t^2 + 20t + 2$ où $h(t)$ est la hauteur en mètres et $t$ est le temps en secondes. -5 est une constante qui représente la gravité. 20 est la vitesse initiale de la boule de feu. 2 est la hauteur initiale de la boule de feu.

Question 1: au bout de combien de temps la boule de feu vas t elle toucher le sol ?

Réponse 1:

• $f(t) = -5t^2 + 20t + 2$

Si $f(t) = 0$:

• $0 = -5t^2 + 20t + 2$

$$-5t^2 + 20t + 2 = 0$$ $$t = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$ $$t = \frac{-20 \pm \sqrt{20^2 - 4*-5*2}}{2*-5}$$ $$t = \frac{-20 \pm \sqrt{400 + 40}}{-10}$$ $$t = \frac{-20 \pm \sqrt{440}}{-10}$$ $$t = \frac{-20 \pm 20.98}{-10}$$ $$t = \frac{-20 + 20.98}{-10} = 0.98$$ $$t = \frac{-20 - 20.98}{-10} = 4.98$$

La boule de feu touchera le sol au bout de 0.98s et 4.98s.

Question 2: Quelle est la hauteur maximale de la boule de feu ?

Réponse 2:

• $f(t) = -5t^2 + 20t + 2$

Le sommet est le point S(h, k):

$$h = -\frac{b}{2a}$$ $$k = f(h)$$ $$h = -\frac{20}{2*-5} = 2$$ $$k = f(2) = -5*2^2 + 20*2 + 2 = 42$$

La hauteur maximale de la boule de feu est de 42m.

Question 3: Quelle est la hauteur de la boule de feu au bout de 1s ?

Réponse 3:

• $f(t) = -5t^2 + 20t + 2$

Si $t = 1$:

• $f(1) = -5*1^2 + 20*1 + 2 = 17m$

La hauteur de la boule de feu au bout de 1s est de 17m.

Fonctions racine carrée

Définition : Pour tout $x$ dans $\mathbb{R}$, la fonction racine carrée est définie par $f(x) = \sqrt{x}$.

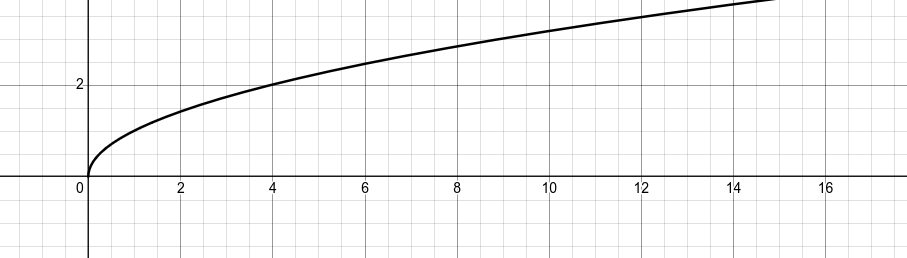
Exemple

Soit la fonction $f(x) = \sqrt{2x+5}$. Trouver l'antécédent de 3.

Réponse:

• $f(x) = \sqrt{2x+5}$
• $f(x) = 3$

Si $f(x) = 3$:

• $\sqrt{2x+5} = 3$

$$2x + 5 = 3^2$$ $$2x + 5 = 9$$ $$2x = 4$$ $$x = 2$$

L'antécédent de 3 est 2.